Turbine1_CL

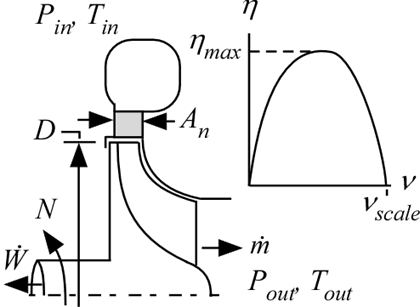
Procedure Turbine1_CL is a model of a low reaction, single-stage radial turbine operating outside of the vapor dome. Mass flow rate is determined from the nozzle area and spouting velocity assuming that all of the pressure drop is across the nozzle. Isentropic efficiency is determined from a generic efficiency (eta) vs velocity ratio (nu) curve. The standard curve is valid from 0 < nu < 1 and provides a maximum efficiency at nu = 1/sqrt(2). The standard curve can be shifted vertically and horizontally.
Inputs:
T_in: inlet temperature (K, C, F, or R)
P_in: inlet pressure (bar, atm, Pa, kPa, MPa)
P_out: outlet pressure (bar, atm, Pa, kPa, MPa)
F$: fluid string identifier
N: rotational speed (rev/s)
eta_max: maximum possible turbine isentropic efficiency (eta vs nu curve is shifted up/down to achieve this)
nu_scale: scales the eta vs nu curve horizontally
a value of 1 applies no scaling - peak of efficiency occurs at nu = 1/sqrt(2)
a value of 1.1 stretches the curve out by 10%
D: diameter (ft or m)
A_n: nozzle area (ft^2 or m^2)
Outputs
m_dot: mass flow rate (kg/s or lb_m/hr)
T_out: outlet temperature (K, C, F, or R)
W_dot: power (W, kW or Btu/hr)
nu: blade to spouting velocity ratio
eta: isentropic efficiency
Ma: Mach number (evaluated at inlet)
Example:
$Load Component LIbrary
$UnitSystem SI Mass J K Pa
$VarInfo m_dot units=kg/s
$VarInfo T_out units=C
$VarInfo W_dot units=W
T_in=1470 [K] "inlet temperature"
P_in=220000 [Pa] "inlet pressure"
P_out=101325 [Pa] "outlet pressure"
F$='Air' "fluid"
N=1700 [rev/s] "rotational speed"
D=0.11 [m] "diameter of turbine"
A_n=0.0001 [m^2] "nozzle area"
eta_max=0.9 [-] "maximum efficiency"
nu_scale=1 "velocity ratio scaling parameter"
Call turbine1_cl(T_in, P_in, P_out, F$, N, D, A_n, eta_max, nu_scale: m_dot, T_out, W_dot, nu, eta, M)
{Solution:
m_dot = 0.0403 [kg/s]
T_out = 1248 [K]
W_dot = 10708 [W]
nu = 0.76
Ma = 0.79}