CentrifugalPump1

CentrifugalPump1_CL

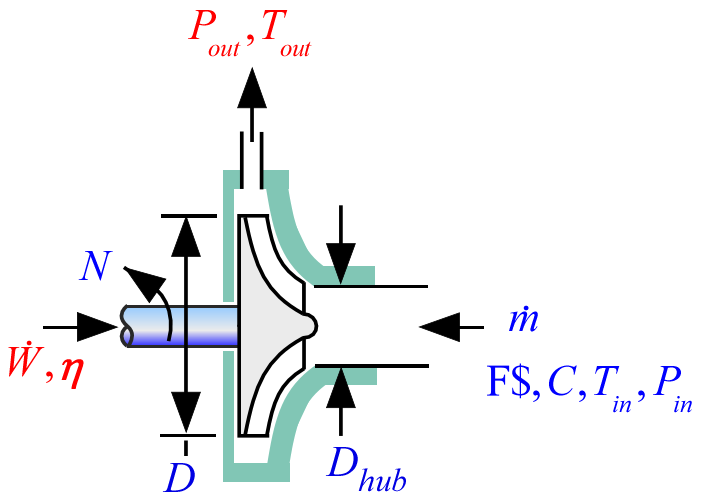
The procedure CentrifugalPump1_CL provides a model of a centrifugal pump that can be used for a real fluid, a brine, or an incompressible fluid. Pumping performance is obtained from a correlation of dimensionless pressure rise as a function of head coefficient curve that is based on data from several manufacturers and pumps. The power performance is obtained from dimensionless power as a function of dimensionless flow curve also based on these data.

Inputs:

F$: fluid string identifier

C: concentration (%) {only used if the fluid is a brine; otherwise set C=0}

T_in: inlet temperature (K, C, F, or R)

P_in: inlet pressure (bar, atm, Pa, kPa, MPa)

m_dot: mass flow rate (kg/s or lb_m/hr)

N: rotational speed (1/s)

D: tip diameter (m or ft)

D_hub: hub diameter (m or ft)

Outputs:

P_out: outlet pressure (bar, atm, Pa, kPa, MPa)

T_out: outlet temperature (K, C, F, or R)

W_dot: power (W, kW or Btu/hr)

eta: efficiency

Example:

$Load Component Library

$UnitSystem SI Mass J K Pa

$VarInfo P_out units=Pa

$VarInfo T_out units=C

$VarInfo W_dot units=W

C=20 [%]

F$='EG'

T_in=300 [K]

P_in=100000 [Pa]

m_dot=2 [kg/s]

N=1700 [1/min]*convert(1/min,1/s)

D=0.15 [m]

D_hub=0.08 [m]

Call centrifugalpump1_cl( F$, C, T_in, P_in, m_dot, N, D, D_hub: P_out, T_out, W_dot, eta)

{Solution:

P_out = 211586 [Pa]

T_out = 300 [K]

W_dot = 381.2 [W]

eta= 0.5729}