Contents - Index

Sample Problem Solution

You need to develop a solution to the problem in EES that uses the variable names and units called out in the problem statement.  My solution is below.

$UnitSystem SI Mass J K Pa

$TabStops 4 in

"Inputs"

P_1_kPa = 300 [kPa]

Vol_1 = 1 [m^3]

"Part a: what is the mass, m_1 (kg)"

P_1=P_1_kPa*Convert(kPa,Pa) "initial pressure"

T_1=ConvertTemp(C,K,20 [C]) "initial temperature"

v_1=Volume(R134a,T=T_1,P=P_1) "specific volume"

m_1=Vol_1/v_1 "initial mass"

"Part b: how much mass is removed, m_out_12 (kg)"

Vol_2=Vol_1*0.2 "volume at state 2"

P_2=P_1 "pressure at state 2"

T_2=ConvertTemp(C,K,20 [C]) "temperature at state 2"

v_2=Volume(R134a,T=T_2,P=P_2) "specific volume"

m_2=Vol_2/v_2 "mass at state 2"

0=m_out_12+m_2-m_1 "mass balance, m_out_12 is the mass extracted during process 1 to 2"

"Part c: pressure after 50% of the remaining mass is removed, P_3_kPa (kPa)"

m_out_23=0.5*m_2 "half of the remaining mass is extracted"

0=m_out_23+m_3-m_2 "mass balance"

Vol_3=Vol_2

T_3=ConvertTemp(C,K,20[C]) "temperature"

v_3=Vol_3/m_3 "specific volume"

P_3=Pressure(R134a,T=T_3,v=v_3) "pressure"

P_3_kPa = P_3*Convert(Pa,kPa) "pressure in kPa"

"Part d: temperature when condensation begins T_4_C (C)"

"Part e: pressure when condensation begins P_4_kPa (kPa)"

v_4=v_3 "specific volume"

x_4=1 "quality"

P_4=Pressure(R134a,x=x_4,v=v_4) "pressure"

P_4_kPa = P_4*Convert(Pa,kPa) "pressure in kPa"

T_4=Temperature(R134a,x=x_4,v=v_4) "temperature"

T_4_C = ConvertTemp(K,C,T_4) "temperature in C"

"Part f: quality when temperature reaches -35 C"

T_5 = ConvertTemp(C,K,-35 [C]) "temperature"

v_5 = v_4 "specific volume"

x_5 = Quality(R134a,T=T_5,v=v_5) "quality"

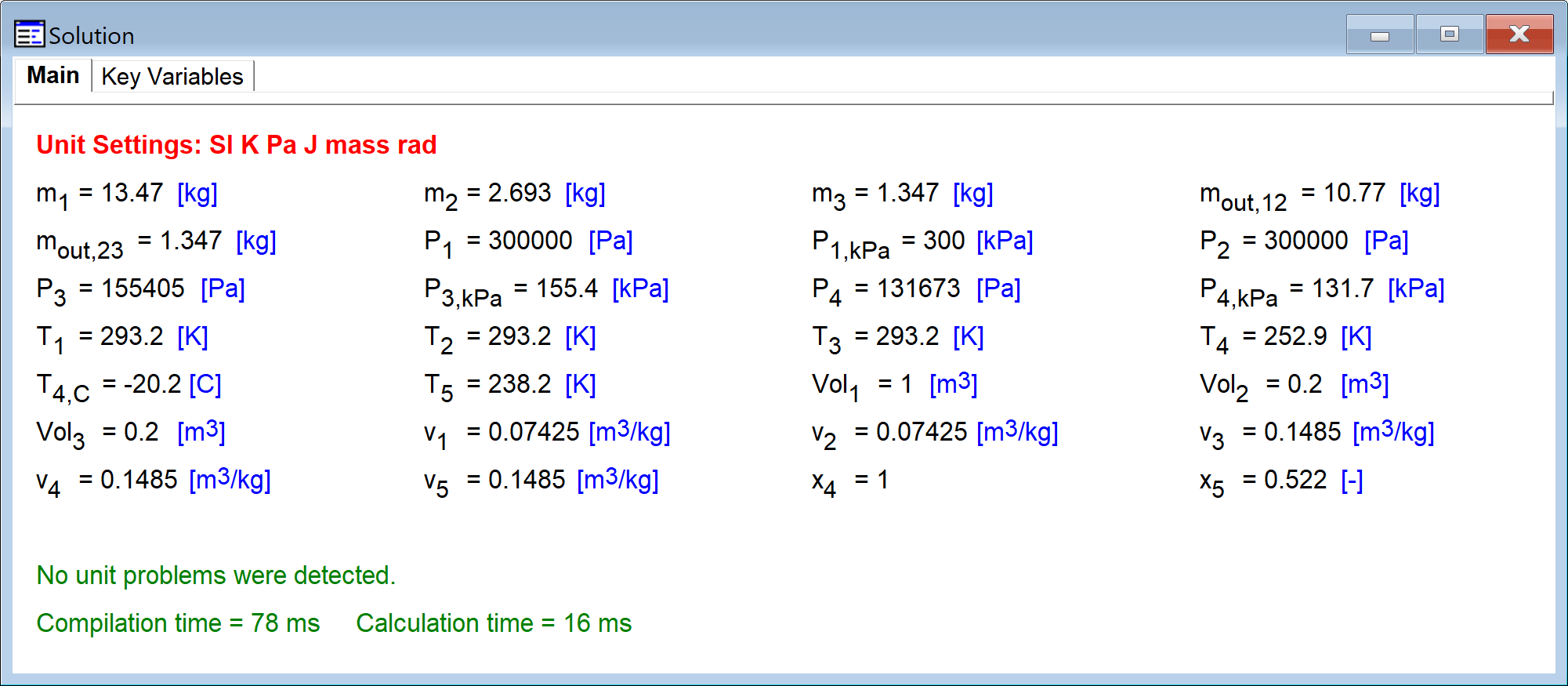
The solution is shown below.