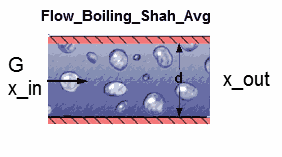
Flow_Boiling_Shah_Avg

Function Flow_Boiling_Shah_avg(Fluid$, T_sat, G, d, x_1, x_2, q``, OR$) calculates the average heat transfer coefficient for boiling of a two-phase fluid inside a circular tube entering with of vapor at quality x_in and exiting with quality x_out .
Inputs
Fluid$ - string variable representing a real fluid in the EES data base.
T_sat - the saturation temperature of the incoming vapor in [C], [K, [F] or [R] (units depend on unit system selected in EES).
G - mass velocity, i.e., the ratio of the mass flow rate to the cross-sectional area of the tube [kg/s-m^2] or [lbm/hr-ft^2]
d - diameter of the tube [m] of [ft]
x_in - quality at inlet (must be between 0 and 1)
x_out - quality at exit (must be between 0 and 1)
q`` - surface heat flux [W/m^2] or [Btu/hr-ft^2]
OR$ - a string constant or variable that must be either 'HORIZONTAL' or 'VERTICAL'
Output
Flow_Boiling_avg - average heat transfer coefficient [W/m^2-K] or [Btu/hr-ft^2-F] including convective and nucleate boiling contributions over the specified range of quality.
Notes:
This procedure uses the Flow_Boiling_Shah procedure to supply values for the local heat transfer coefficient and wall temperature at discrete values of quality. It then integrates these values over the range of quality and returns the integrated average heat transfer coefficient.
Example:
$UnitSystem SI K Pa J
$TabStops 3.5 in
$varInfo h_bar units=W/m^2-K
$VarInfo q`` units=W/m^2
$VarInfo U units=W/m^2-K
F$='R22'
T_sat=250 [K] "boiling saturation temperature"
G=200 [kg/m^2-s] "mass velocity"
d=0.0172 [m] "tube inner diameter"
x_in=0.36 "quality"
x_out=1.00
h_bar=flow_boiling_shah_avg(F$,T_sat, G, d, x_in, x_out, q``, 'horizontal')
q``=U*(T_h-T_sat) "heat flux"
T_h=261 [K] "temperature of fluid on outside of pipe"
h_h=5400 [W/m^2-K] "heat transfer coefficient on outside surface of pipe"
U=(1/h_bar+1/h_h)^(-1) "overall heat transfer coefficient between fluids on either side of the pipe wall"
{Solution:
h_bar=2,490 [W/m^2-K]}