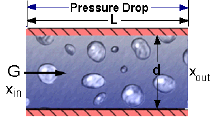
Pressure Drop in Horizontal Tubes

Function DELTAP_2phase_horiz returns the two-phase pressure drop in a horizontal tube.
Inputs:
Fluid$ - a string constant or variable with the name of a fluid/vapor in the EES database
G - mass velocity, i.e., the ratio of the mass flow rate to the cross-sectional area of the tube [kg/s-m^2] or [lbm/hr-ft^2]
P_i - entering saturation pressure of the fluid in [Pa, kPa, bar, MPa] or [psia, atm] depending on the choice of EES unit system
d - inside diameter of the tube in [m] or [ft]
L - length of the tube in [m] or [ft]
x_in - quality at the fluid inlet (0<=x_in<=1)
x_out - quality at the fluid outlet (0<=x_out<=1)
Output:
DELTAP_2phase_horiz - pressure drop in[Pa, kPa, bar, MPa] or [psia, atm]
Notes:
The pressure drop (DELTAP) is the sum of the frictional pressure drop and the momentum pressure drop. The momentum pressure drop is calculated using a void fraction obtained from drift flux model, as described by Ould Didi et al. (2002).
The Muller-Steinhagen and Heck correlation described by Ould Didi et al. (2002) is used to predict the pressure gradient. The pressure gradient is then integrated to determine the pressure drop from inlet to outlet. The heat flux is assumed to be constant along the length of the tube so that dL/dx is constant.
Example:
R134a enters a 12 mm tube of an evaporator at a mass flow rate of 0.036 kg/s with an inlet quality of 0.35. The evaporator is 1 m in length and the R134a exits as saturated vapor. Estimate the pressure drop.
$unitSystem SI K Pa J
$VarInfo A units=m^2
$VarInfo G units=kg/s-m^2
$VarInfo P_i units=Pa
$VarInfo DELTAP units=Pa
Fluid$='R134a'
d=12 [mm]*convert(mm,m)
P_i=pressure(Fluid$,T=converttemp(C,K,4 [C]),x=0)
L=1[m]
x_in=0.35
x_out=1.0
m_dot=0.036 [kg/s]
A=pi*d^2/4
G=m_dot/A
DELTAP=deltap_2phase_horiz(Fluid$,G,P_i,d,L,x_in, x_out)
{Solution: DELTAP=9127Pa}