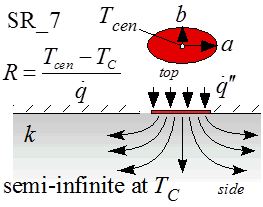
SR_7

Function SR_7(a, b, n, k) returns the thermal resistance between the surface of a hyperellipse contact area that is exposed to a uniform heat flux and is located on the surface of a semi-infinite half-space. The resistance is based on the center temperature of the ellipse. A hyperellipse is defined by the equation:
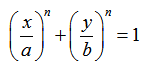
where a is the major radius and b is the minor radius (a >= b ). When n = 2 the hyperellipse is just an ellipse and when a = b and n = 2 the hyperellipse becomes a circle. Larger values of n result in a more rectangular shape with rounded edges. The limits of the solution are:
0.1 < a/b < 1
n > 0.5
The calling protocol is:
R = SR_7(a, b, n, k)
Inputs:
a = major radius of the ellipse [m or ft]
b = minor radius of the ellipse [m or ft]
n = ellipse parameter
k = thermal conductivity of the material [W/m-K or Btu/hr-ft-R]
Outputs:
R = resistance [K/W or R-hr/Btu]
Rohsenow, W.M, J. P. Hartnett, and Y. I. Cho, Handbook of Heat Transfer, 3rd Edition, McGraw Hill, (1998).
Example:
$UnitSystem SI Mass J K Pa Radian
$VarInfo R3 units=K/W
$VarInfo R7 units=K/W
a=1 [m]
b=1 [m]
n=2
k=1 [W/m-K]
R7=sr_7(a,b,n,k)
R3=sr_3(a,k)
{Solution:
R7=R3 = 0.3183 [K/W]}