SR_13

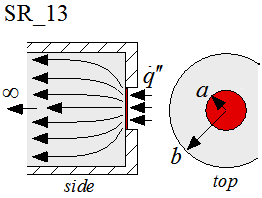
Function SR_13(a, b, k) returns the thermal resistance associated with spreading between a circular contact area located on the surface of an infinitely long circular flux tube. The spreading resistance is the thermal resistance that is in addition to the 1-D thermal resistance in the flux tube that would exist if the heat flux was applied uniformly over the entire area of the tube. The resistance is based on the average temperature over the area. The contact area itself is assumed to be exposed to a uniform heat flux.
Note that if a << b then the result approaches the equivalent result for spreading resistance from a half-space given by SR_2.
Note that the total resistance associated with conduction through a circular bar of length L with a contact on one end will be the sum of the normal, 1D resistance and the spreading resistance:
R_total = L/(k*pi*b^2) + SR_13 (SR_13 only calculates the additional resistance associated with spreading that occurs at the end of the bar)

The calling protocol is:
R = SR_13(a, b, k)
Inputs:
a = radius of contact area [m or ft]
b = radius of flux tube [m or ft]
k = thermal conductivity of the material [W/m-K or Btu/hr-ft-R]
Outputs:
R = spreading resistance [K/W or R-hr/Btu]
Rohsenow, W.M, J. P. Hartnett, and Y. I. Cho, Handbook of Heat Transfer, 3rd Edition, McGraw Hill, (1998).
Example:
$UnitSystem SI Mass J K Pa Radian
$VarInfo R13 units=K/W
a=1 [m]
b=2 [m]
k=1 [W/m-K]
R13=sr_13(a,b,k)
{Solution:
R13 = 0.1023 [K/W]}