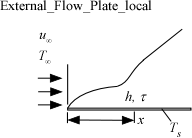
External_Flow_Plate_local

Procedure External_Flow_Plate_local(Fluid$, T_inf, T_s, P, V, L: tau, h, C_f, Nusselt, Re) calculates the local heat transfer coefficient and the local shear stress for external flow over a flat plate. The properties are evaluated at the film temperature and the units of the inputs and outputs correspond to the settings in EES. (Note that the shear stress is returned in either Pa or psi units.)
Inputs
Fluid$ can be any fluid in the EES data base. The fluid can be an ideal gas, a real fluid, a brine, or an incompressible fluid in the Solid-Liquid_Props fluids library.
T_inf - the free stream fluid temperature in [C], [K], [F], or [R].
T_s - the surface temperature of the plate in [C], [K], [F], or [R].
P - pressure can be in [Pa], [kPa], [bar], [MPa], [atm], or [psia]. (Note that for brines, this parameter provides the concentration in % instead of pressure.)
u_inf - free stream velocity of flow in [m/s] or [ft/min]
x - position on the plate in [m] or [ft]
Outputs
tau - local shear stress [Pa] or [psi]
h - local heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R]
C_f - local coefficient of friction [-], defined as:
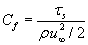
where
r is the density of the fluid
Nusselt - local Nusselt number [-], defined as:
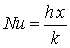
where
k is the conductivity of the fluid
Re - Reynolds number [-], defined as:
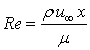
where
m is the viscosity of the fluid
Notes
This procedure determines the property data of the specified fluid and calculates the Reynolds and Prandtl numbers. The Prandtl, Reynolds and Nusselt numbers are based on the film temperature, which is the average of the free stream and the surface temperatures. This procedure then passes the Reynolds and Prandtl numbers to the non-dimensional procedure External_Flow_Plate_ND_local. The non-dimensional procedure then returns the values for C_f and Nusselt and External_Flow_Plate_local calculates the local shear stress and the convection heat transfer coefficient.
Note that the procedure External_Flow_Plate_L_local provides the same functionality but uses the more accurate correlations described by Lienhard (2020) that include the impact of the transition region.
Example:
$unitSystem SI K Pa J
$VarInfo h units=W/m^2-K
$VarInfo tau units=Pa
T_s=328 [K]
Fluid$='air'
T_inf=297 [K]
P=101300 [Pa]
u_inf=7 [m/s]
L=0.5 [m]
Call external_flow_plate_local(Fluid$, T_inf, T_s, P, u_inf, L: tau, h, C_f, Nusselt, Re)
{Solution:
C_f=0.001462
h=7.076 [W/m^2-K]
Nusselt=133.1
Re=206382
tau=0.04044 [Pa]
}