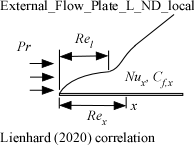
External_Flow_Plate_L_ND_local

Procedure External_Flow_Plate_L_ND_local(Re, Pr, Re_l: Nusselt, C_f) returns the local Nusselt number and local friction coefficient for flow parallel to a flat plate using the Lienhard correlation.
Inputs:
Re - local Reynold's number [-], where
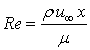
where
r is the density of the fluid
m is the viscosity of the fluid
x is the position relative to the leading edge of the plate
u_infinity is the velocity of the flow
Pr - Prandtl number [-], where
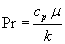
where
c_p is the specific heat capacity of the fluid
k is the conductivity
Re_l - local Reynolds number [-] where transition region starts (3x103 < Re_l < 5x105)
Note that if the value of Re_l is < 0 then it is interpreted as the turbulence intensity (u`/u, as a percentage)
In this case, the empirical equation from Mayle (1991) is used.
Outputs:
Nusselt - local Nusselt number assuming a constant wall temperature[-]. The Nusselt number is defined:
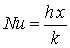
where
h is the average heat transfer coefficient
C_f - local friction coefficient [-]. The friction coefficient is defined:
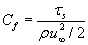
where
t is the local shear stress
Notes
This procedure uses the methodology presented by Lienhard (2020) to determine the local Nusselt number. The methods are adapted to also provide the local friction coefficient. Both cases more rigorously consider the transitional region. When the flow is laminar, the local Nusselt number is obtained using the Churchill and Ozoe (1973) correlation as presented in section 4.9.2 of Nellis and Klein. This correlation is valid for all Prandtl numbers provided that the Peclet number is larger than about 100. When the flow is turbulent the Nusselt number and friction factor are both evaluated using the correlations provided by Lienhard (2020).
The Reynolds and Prandtl numbers are based on fluid properties evaluated at the film temperature, which is the average of the free stream and the surface temperatures.
Example:
Re_l=1e5
Re=1e6
Pr=0.7
Call external_flow_plate_l_nd_local(Re,Pr,Re_l: Nusselt,C_f)
{Solution:
C_f=0.003759
Nusselt=1489
}