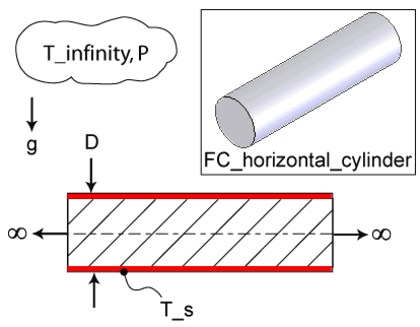
FC_horizontal_cylinder

The procedure FC_horizontal_cylinder(Fluid$, T_s, T_infinity, P, D : h, Nusselt, Ra) returns the heat transfer coefficient, Nusselt number and Rayleigh number for an infinitely long horizontal cylinder of diameter D. In practice, the cylinder need only be long enough so that the end effects are negligible (~L/D = 5). The units of the inputs and outputs depend on the unit settings in EES. The magnitude of gravity is assumed to be 9.807 [m/s^2].
Inputs:
Fluid$ - string name of any fluid in the EES database. The fluid can be an ideal gas or a real fluid
T_s - surface temperature of the plate in [C], [K], [F], or [R].
T_infinity - bulk temperature of the fluid in [C], [K], [F], or [R].
P - ambient pressure in [Pa], [kPa], [bar], [MPa], [atm], or [psia]
D - diameter of the cylinder [m] or [ft]
Outputs:
h - heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R]
Nusselt - Nusselt number [-]
Ra - Rayleigh number [-]
Notes:
The procedure FC_horizontal_cylinder is responsible for determining the fluid properties and calculating the Rayleigh and Prandtl number. Once these values are found, the non-dimensional procedure FC_horizontal_cylinder_ND is called to calculate the Nusselt number. FC_horizontal_cylinder, in turn, uses the Nusselt number to calculate the heat transfer coefficient as described in section 6.2.4 of Nellis and Klein.
Example:
$UnitSystem SI deg K J Pa
$VarInfo h units=W/m^2-K
P=101300 [Pa]
T_s=315 [K]
T_infinity=300 [K]
D=0.09 [m]
Fluid$='water'
Call fc_horizontal_cylinder(Fluid$, T_s, T_infinity, P, D : h, Nusselt, Ra)
{Solution:
h=695.4 [W/m^2-K]
Nusselt=100.8
Ra=3.335E+08}