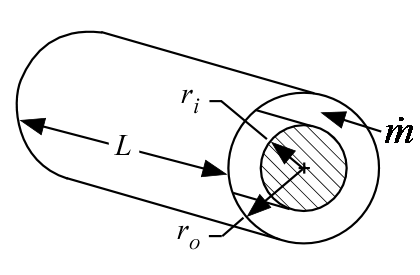
AnnularFlow

Procedure AnnularFlow( Fluid$, T, P, m_dot, r_i, r_o, L, RelRough: h_T, h_H, DELTAP, Nusselt_T, f, Re) returns the lower and upper bounds on the convection coefficient for developing or fully-developed flow in an annular duct. The outer wall of the annulus is assumed to be insulated so heat transfer occurs across the wall separating the annulus from the pipe. The area used for heat transfer should be the area of this wall. The procedure also returns the friction factor for these conditions.
Inputs:
Fluid$ can be any fluid in the EES database. The fluid can be an ideal gas, real fluid, brine or fluid in the Solid-Liquid property library.
T - the bulk temperature of the fluid [C], [K], [F], or [R].
P - pressure can be in [Pa], [kPa], [bar], [MPa], [atm], or [psia]. (Note that for brines, this parameter provides the concentration in % instead of the pressure)
m_dot - mass flow rate in [kg/s] or [lbm/hr]
r_i - inner radius of annulus [m] or [ft]
r_o - outer radius of annulus [m] or [ft]
L - length of the annulus [m] or [ft]
RelRough - the ratio of the dispersions on the walls of the duct to the hydraulic diameter of the duct (must be between 0 and 0.05). The hydraulic diameter is 2 (r_o - r_i).
Outputs:
h_T - lower bound heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R] assuming that the inner annulus wall is at constant temperature
h_H - upper bound on heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R] assuming a constant heat flux at the inner annulus wall
DELTAP - pressure difference between the inlet and outlet of the annular space in the pressure units set in the EES Unit System dialog
Nusselt_T - Nusselt number corresponding to the lower heat transfer coefficient.l
f - friction factor [-]
Re - Reynolds number
Notes:
This procedure calculates the Reynolds and Prandtl numbers and then calls AnnularFlow_N which determines the Nusselt numbers based on boundary conditions of constant temperature and constant heat flux individually.
Two values of the heat transfer coefficient are returned that should provide upper and lower bounds. These heat transfer coefficients are both for the inner annular wall with an insulated outer wall. For turbulent flow, these values are identical.
The procedure will determine if the flow is laminar or turbulent. Transitional flow is assumed to occur for Reynold's numbers between 2300 and 3000 and interpolation is applied between the laminar and turbulent correlations.
Example 1:
$unitSystem SI Pa K J
$VarInfo DELTAP units=Pa
$VarInfo h_H units=W/m^2-K
$VarInfo h_T units=W/m^2-K
$TabStops 2 in
T=363 [K] "average temperature of fluid in duct"
P=101300 [Pa] "pressure of air in annulus"
m_dot=0.001 [kg/s] "flow rate"
r_i=0.01 [m] "inner radius"
r_o=0.025 [m] "outer radius"
L=5 [m] "length"
RelRough=0.005 [-] "relative roughness"
Call annularflow('air',T,P,m_dot,r_i, r_o,L,RelRough:h_T, h_H ,DELTAP, Nusselt_T, f, Re)
{Solution:
h_T=6.460 [W/m^2-K]
h_H=6.818 [W/m^2-K]
DELTAP=3.73 [Pa]
Nusselt_T=6.411 [-]
f=0.1184 [-]}
Note that it is not necessary to evaluate all outputs for versions 9.513 or newer. For example, if only h_H is of interest, the call statement can be:
call AnnularFlow('air',T,P,m_dot,r_i, r_o,L,RelRough:, h_H , , , , )
Example 2:
$unitSystem SI Pa K J
$VarInfo DELTAP units=Pa
$VarInfo h_H units=W/m^2-K
$VarInfo h_T units=W/m^2-K
$TabStops 2 in
T=363 [K] "average temperature of fluid in duct"
C=50[%] "concentration of the propylene glycol-water brine solution"
m_dot=0.25 [kg/s] "flow rate"
r_i=0.01 [m] "inner radius"
r_o=0.025 [m] "outer radius"
L=5 [m] "length"
RelRough=0.005 [-] "relative roughness"
Call annularflow('PG',T,C,m_dot,r_i, r_o,L,RelRough:h_T, h_H ,DELTAP, Nusselt_T, f, Re)
{Solution:
DELTAP=84.87 [Pa]
f=0.04376 [-]
h_H=632.8 [W/m^2-K]
h_T=632.8 [W/m^2-K]
Nusselt_T=47.87}