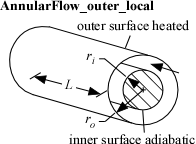
AnnularFlow_outer_local

Procedure AnnularFlow_outer_local( Fluid$, T, P, m_dot, r_i, r_o, L, RelRough: h_T_x, h_H_x, dPdx) returns lower and upper bounds for the local convection coefficient and the local pressure gradient for flow in an annular duct with a heated external surface. The local values are determined at axial position x by numerically differentiating the average values. The inner wall of the annulus is assumed to be insulated so heat transfer occurs across the outer wall. The area used for heat transfer should be the area of this outer wall.
Inputs:
Fluid$ can be any fluid in the EES database. The fluid can be an ideal gas or a real fluid.
T - the bulk temperature of the fluid [C], [K], [F], or [R].
P - pressure can be in [Pa], [kPa], [bar], [MPa], [atm], or [psia].
m_dot - mass flow rate in [kg/s] or [lbm/hr]
r_i - inner radius of annulus [m] or [ft]
r_o - outer radius of annulus [m] or [ft]
x - location along the flow axis [m] or [ft]
RelRough - the ratio of the dispersions on the walls of the duct to the hydraulic diameter of the duct (must be between 0 and 0.05). The hydraulic diameter is 2 W H/(W + H).
Outputs: (all but the first output are optional)
h_T_x - lower bound on the local heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R] assuming that the outer annulus wall is at constant temperature
h_H_x - upper bound on the local heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R] assuming a constant heat flux at the outer annulus wall
dPdx - local pressure gradient. [(Pa, kPa, bar, or atm)/m] or [(psi or atm)/ft] depending on EES pressure unit setting
Notes:
This procedure determines the local values by differentiating the average values calculated in the AnnularFlow_outer procedure .
Two values of the heat transfer coefficient are returned that provide upper and lower bounds. These heat transfer coefficients are both for the outer annular wall with an insulated inner wall. For turbulent flow, these values are identical.
Example:
$unitSystem SI K Pa J
$VarInfo dPdx units=Pa/m
$VarInfo h_H_x units=W/m^2-K
$VarInfo h_T_x units=W/m^2-K
$TabStops 2 in
T=363 [K] "average temperature of fluid in duct"
P=101300 [Pa] "pressure of air in annulus"
m_dot=0.001 [kg/s] "flow rate"
r_i=0.01 [m] "inner radius"
r_o=0.025 [m] "outer radius"
x=5 [m] "length"
RelRough=0.005 [-] "relative roughness"
Call annularflow_local('air', T, P, m_dot, r_i, r_o, x, RelRough:h_T_x, h_H_x, dPdx)
{Solution:
dPdx=-0.704 [Pa/m]
h_H_x=6.598 [W/m^2-K]
h_T_x=6.205 [W/m^2-K]}