Contents
- Index
Convection
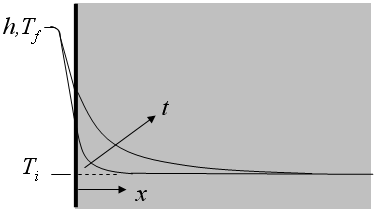
Function semiinf3(T_i,T_f,h,k,alpha,x,time) returns the temperature for a given position and time within a semi-infinite body with surface convection using the relation provided in Table 3-2 of Nellis and Klein.
Inputs:
T_i - initial temperature of the solid [C] or [K]
T_f - bulk fluid temperature [C] or [K]
h - convection coefficient [W/m^2-K]
alpha - thermal diffusivity [m^2/s]
x - perpendicular distance from surface [m]
time - time relative to surface exposure (surface convection begins at t=0) [s]
This function can be used with English units set in EES. In this case, T_i and T_f are in [F] or [R], h is in Btu/hr-ft^2-R, alpha is in ft^2/hr and x is in [ft]. Time must be in s.
Example:
$UnitSystem SI K Pa J
$VarInfo T units=K
T_i=393[K]
T_f=355 [K]
h = 50 [W/m^2-K]
alpha=0.000004029 [m^2/s]
k=10 [W/m-K]
x=0.003 [m]
time=100 [s]
T=semiinf3(T_i,T_f,h,k,alpha,x,time)
{Solution:
T=389.5 [K]}
Transient Conduction Index

