Step-change in Surface Convection for Semi-Infinite Body Outside of Sphere

Step-change in Surface Convection for Semi-Infinite Body Outside of Sphere

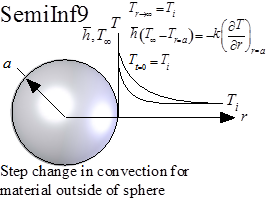
Function SemiInf9(T_i, h_bar, T_infinity, alpha, k, a, r, time) returns the temperature within a semi-infinite material that is located outside of a spherical surface and is subjected to a step change in the convective boundary condition at the surface. Solution is from Carslaw and Jaeger as reported in the Handbook of Heat Transfer.

The calling protocol is:

T=SemiInf9(T_i, h_bar, T_infinity, alpha, k, a, r, time)

Inputs:
T_i = initial temperature of the material [C] or [K]
h_bar = heat transfer coefficient [W/m^2-K]
T_infinity = fluid temperature within the sphere [C] or [K]
alpha = thermal diffusivity [m^2/s]
k = thermal conductivity [W/m-K]
a = radius of sphere [m]
r = radial position [m]
time = time relative to beginning of surface disturbance [s]

This function can be used with English units set in EES. In this case, T_i is in [F] or [R], h_bar is in [Btu/hr-ft^2-R], T_infinity is in [F] or [R], alpha is in [ft^2/hr], k is in [Btu/hr-ft], a is in [ft], r is in [ft], and time is in [s].

Outputs:
T is the temperature in [C] or [K] (or [F] or [R] in English units)

Rohsenow, W.M., J.P. Hartnett, and Y.I. Cho, Handbook of Heat Transfer, 3rd Edition, McGraw Hill, (1998).

Example:
$UnitSystem SI Mass J K Pa
$VarInfo T units=K
T_i=300 [K]
h_bar=100 [W/m^2-K]
T_infinity=500 [K]
alpha=1e-4 [m^2/s]
k=1.5 [W/m-K]
a=0.01 [m]
r=0.02 [m]
time=20 [s]
T=semiinf9(T_i,h_bar, T_infinity, alpha, k, a, r, time)

{Solution:
T=380.1 [K]}

Transient Conduction Index