MOI_Ibeam_ns

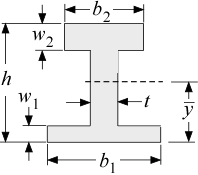
This procedure returns properties of an I-beam that is not symmetric in terms of the upper and lower flanges.
Inputs
h = height [m, ft]
b_1 = width of bottom flange [m, ft]
b_2 = width of top flange [m, ft]
w_1 = height of bottom flange [m, ft]
w_2 = height of top flange [m, ft]
t = thickness of web [m, ft]
Outputs
A = area [m^2, ft^2]
I = moment of inertia [m^4, ft^4]
Z = section modulus [m^3, ft^3]
rho = radius of gyration [m, ft]
y_bar = distance from bottom of beam to neutral axis [m, ft]
Example:
$Load Mechanical Design
$UnitSystem SI K Pa
$VarInfo A units=m^2
$VarInfo I units=m^4
$VarInfo rho units=m
$VarInfo y_bar units=m
$VarINfo Z units=m^3
b_2 = 0.08 [m]
b_1 = 0.04 [m]
h = 0.1 [m]
w_2 =0.02 [m]
w_1 = 0.03 [m]
t = 0.015 [m]
Call moi_ibeam_ns(h, b_1, b_2 , w_1, w_2 ,t: A, I, Z, rho, y_bar)
{Solution:
A = 0.00355 m^2
I = 4.162e-6 m^4
Z = 7.269e-5 m^3
rho = 0.03424 m
y_bar = 0.05725 m
}
Reference: Marks' Standard Handbook for Mechanical Engineers, 10th Edition, Avallone, E. A. and T. Baumeister III, eds., McGraw Hill, (1996).