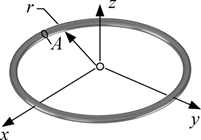
MOI_ThinRing

This procedure returns mass and moments of inertia of a straight thin rod bent into a ring
Inputs
r = radius of the ring [m, ft]
A = cross-sectional area of rod [m^2, ft^2]
rho = material density [kg/m^3, lbm/ft^3]
Outputs
m=mass [kg, lb_m]
I_x = moment of inertia about the x-axis [kg-m^2 or lbm-ft^2]
I_y= moment of inertia about the y-axis [kg-m^2 or lbm-ft^2]
I_z = moment of inertia about the z-axis [kg-m^2 or lbm-ft^2]
Example:
$Load Mechanical Design
$UnitSystem SI K Pa
$VarInfo I_x units=kg-m^2
$VarInfo I_y units=kg-m^2
$VarInfo I_z units=kg-m^2
r = 0.25 [m]
A = 1e-4 [m^2]
rho=990 [kg/m^3]
Call moi_thinring(A, r, rho: m, I_x, I_y, I_z)
{Solution:
m = 0.1555 [kg]
I_x= 0.00486 [kg-m^2]
I_y= 0.00486 [kg-m^2]
I_z = 0.009719 [kg-m^2]
}
Reference: Gray, G.L, F. Costanzo, R.J. Witt, and M.E. Plesha, Engineering Mechanics: Statics and Dynamics, Third Edition, McGraw Hill, (2023).