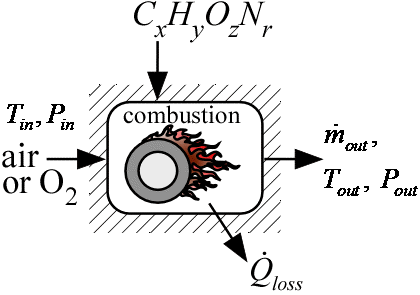
Combustor3_CL
Procedure Combustor3_CL provides a model of a combustor. It accepts the name of the fuel, which can be a name contained in the list of ideal and NASA gases or any chemical formula consisting of elements C, H, O, and N. The procedure assumes complete combustion with dry air or pure oxygen. No fuel remains. The percentage of excess air (or oxygen) above the stoichiometric requirement is provided in input Excess%. At the elevated temperatures occurring in a combustion process, dissociation reactions that produce CO, NO, OH and other species can occur to a significant extent and they affect the outlet temperature of the combustion of the product gas. This model is specifically designed to consider dissociation reactions. The product gas is assumed to be a mixture of CO2, CO, H2O, H, H2, OH, O ,O2 ,NO, NO2, N2 and N, and the mole fractions of these gases are determined in the analysis.
The fuel is assumed to be supplied at the same temperature as the air. Some of the energy released in the combustion process may be transferred to the surrounding through the combustor jacket. The rate of energy transfer from the combustion chamber is calculated as the product of a Conductance and the difference in temperature between the outlet gas and in the inlet air. The procedure returns the this energy transfer rate and the rate of energy transfer that would occur if the combustion gases were cooled from their outlet temperature to the inlet temperature of the air used for combustion.
An efficiency (Eff) is determined as the ratio of the energy in the product gas to the lower heating value of the fuel. Note that, even when the Conductance is 0 so that there are no energy losses from the combustion chamber, Eff may be less than one as a result of the dissociation reactions.
Inputs:
F$: Name of a fuel or fuel mixture consisting of C, H, O, and N, e.g., C4H10 or 0.95*CH4+0.05*C2H6. Natural_gas is also accepted.
LHV: average lower heating value of the fuel (J/kg, kJ/kg, Btu/lb_m) (set to 0 if F$ is an EES substance)
T_in: inlet temperature of air and fuel (K, C, F, or R)
P_in: inlet pressure of air (bar, atm, Pa, kPa, MPa)
OX$: string constant or string variable that is set to either 'Air' or 'O2'
m_dot_fuel: inlet mass flow rate of fuel (kg/s or lb_m/hr) {note that this differs from Combustor2_CL}
Excess%: Percent excess air - 0 is stoichiometric. Must be >=0
DPoverP: pressure loss in combustor normalized by inlet pressure
Conductance: conductance of combustor vessel (W/K or Btu/hr-R) Set to 0 if no heat loss.
Outputs:
m_dot_out: outlet mass flow rate of combustion gases(kg/s or lb_m/hr)
T_out: outlet temperature (K, C, F, or R)
P_out: outlet pressure (bar, atm, Pa, kPa, MPa)
Q_dot_f: rate of heat transfer if product gases are cooled to T_in (W, kW or Btu/hr)
Q_dot_loss: rate of heat transfer to ambient (W, kW, or Btu/hr)
Eff: Combustor efficiency defined as Q_dot_f/LHV
AF: ratio of the mass flow rate of air (or oxygen) to the mass flow rate of fuel
x[1..12] mole fractions of CO2, CO, H2O, H, H2, OH, O ,O2 ,NO, NO2 ,N2 and N
Only the first three outputs are required.
Note: F$ identifies the composition of the fuel. F$ can be set to any recognized EES substance in the built-in ideal gas or NASA library provided the substance is composed of elements C, H, O and N. In addition, a mixture can be specified by using the + symbol with each species multiplied by its mole fraction. For example to specify a mixture of 95% CH4 and 5% CO2, set F$ to 0.95*CH4+0.05*CO2. However, if F$ is not a recognized fluid name, it is necessary to provide the lower heating value of the fuel per unit MASS of the fuel mixture.
Example 1: {Combustion of butane with 10% excess air}
$Load Component Library
$UnitSystem SI C kPa mass kJ
$VarInfo P_out Units=kPa
$VarInfo T_out Units=C
$VarInfo MW Units=kg/kmol
$VarInfo m_dot_out Units=kg/s
$VarInfo Q_dot_f Units=kW
$VarInfo Q_dot_loss Units=kW
T_in=25 [C]
P_in=101.3 [kPa]
m_dot_fuel=0.0005 [kg/s] "mass flow rate of fuel"
Excess%=10 [%]
DPoverP=0.02
Conductance=0 [kW/K]
F$='C4H10'
LHV=0 [kJ/kg]{specify 0 so EES uses the known LHV for this fluid}
OX$='air'
Call combustor3_cl(F$, LHV, T_in, P_in, OX$, m_dot_fuel, Excess%, DPoverP, Conductance: m_dot_out, T_out, P_out, Q_dot_f, Q_dot_loss,eff, AF, MW, x[1..12], C$[1..12])
{Solution:
AF=16.78
eff=0.9772
m_dot_out=0.00889 [kg/s]
P_out=99.27 [kPa]
Q_dot_f=22.16 [kW]
Q_dot_loss=0 [KW]
T_out=1876 [C]
"Mole fractions, x[1..12]"
CO2 0.1085
CO 0.001446
H2O 0.1348
H 0.00008009
H2 0.0003517
OH 0.004427
O 0.0006223
O2 0.01588
NO 0.002971
NO2 0.000002823
N2 0.7309
N 2.311E-09
}
Example 2: {Combustion of ammonia with stoichiometric O2}
$Load NASA
$Load Component
$UnitSystem SI K kPa mass kJ
$VarInfo P_out Units=kPa
$VarInfo T_out Units=C
$VarInfo MW Units=kg/kmol
$VarInfo m_dot_out Units=kg/s
$VarInfo Q_dot_f Units=kW
$VarInfo Q_dot_loss Units=kW
T_in=298.15 [K]
P_in=101.3 [kPa]
m_dot_fuel=0.00025 [kg/s] "mass flow rate"
Excess%=0 [%]
DPoverP=0.0
Conductance=0.0 [kW/K]
F$='NH3'
LHV=22500 [kJ/kg]
OX$='O2'
Call combustor3_cl(F$, LHV, T_in, P_in, OX$, m_dot_fuel, Excess%, DPoverP, Conductance: m_dot_out, T_out, P_out, Q_dot_f, Q_dot_loss, eff, AF)
{Solution:
AF=1.412
eff=0.6417
m_dot_out=0.0006029 [kg/s]
P_out=101.3 [kPa]
Q_dot_f=3.609 [kW]
Q_dot_loss=0 [KW]
T_out=3005 [K]
}
Example 3: {Combustion of natural gas}
$Load Component Library
$UnitSystem SI C kPa mass kJ
$VarInfo P_out Units=kPa
$VarInfo T_out Units=C
$VarInfo MW Units=kg/kmol
$VarInfo m_dot_out Units=kg/s
$VarInfo Q_dot_f Units=kW
$VarInfo Q_dot_loss Units=kW
$VarInfo MW Units=kg/kmol
T_in=25 [C]
P_in=101.3 [kPa]
m_dot_fuel=0.0005 [kg/s] "mass flow rate of fuel"
Excess%=10 [%]
DPoverP=0.02
Conductance=0 [kW/K]
F$='Natural_Gas'
LHV=0 {specify 0 so EES uses the known LHV for this fluid}
Call combustor3_cl(F$, LHV, T_in, P_in, 'air', m_dot_fuel, Excess%, DPoverP, Conductance: m_dot_out, T_out, P_out, Q_dot_f, Q_dot_loss, eff, AF, MW, x[1..12])
{Solution:
AF=17.39
Conductance=0 [kW/K]
DPoverP=0.02
eff=0.9807
Excess%=10 [%]
F$='Natural_Gas'
LHV=0
m_dot_fuel=0.0005 [kg/s]
m_dot_out=0.009196
MW=27.74 [kg/kmol]
P_in=101.3 [kPa]
P_out=99.27
Q_dot_f=22.82
Q_dot_loss=0
T_in=25 [C]
T_out=1833
}
Example 4:(Combustion of a mixture of 25% Methane and 75% Nitrogen on a molar basis}
$Load Component Library
$UnitSystem SI C kPa mass kJ
$VarInfo P_out Units=kPa
$VarInfo T_out Units=C
$VarInfo MW Units=kg/kmol
$VarInfo m_dot_out Units=kg/s
$VarInfo Q_dot_f Units=kW
$VarInfo Q_dot_loss Units=kW
$VarInfo MW Units=kg/kmol
T_in=25 [C]
P_in=101.3 [kPa]
m_dot_fuel=0.0005 [kg/s] "mass flow rate of fuel"
Excess%=1 [%]
DPoverP=0.02
Conductance=0 [kW/K]
F$='0.25*CH4+0.75*N2' "25% CH4 on a molar basis"
LHV=0.25 [kmol]*molarmass(CH4)*lowerheatingvalue(CH4)/(0.25 [kmol]*molarmass(CH4)+0.75 [kmol]*molarmass(N2)) "LHV per kg of mixture"
Call combustor3_cl(F$, LHV, T_in, P_in, 'air', m_dot_fuel, Excess%, DPoverP, Conductance: m_dot_out, T_out, P_out, Q_dot_f, Q_dot_loss, eff, AF, MW, x[1..12])
{Solution:
AF=2.756
Conductance=0 [kW/K]
DPoverP=0.02
eff=0.9947
Excess%=1 [%]
F$='0.25CH4+0.75N2'
LHV=8018 [kJ/kg]
m_dot_fuel=0.0005 [kg/s]
m_dot_out=0.001878 [kg/s]
MW=27.71 [kg/kmol]
P_in=101.3 [kPa]
P_out=99.27 [kPa]
Q_dot_f=3.988 [kW]
Q_dot_loss=0 [kW]
T_in=25 [C]
T_out=1612 [C]
}
See also: Combustor1