STUDENTS

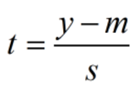
STUDENTS_T

The Students_T function(t, degfreedom) returns the confidence level or probability that a value y is within a normally distributed distribution with mean m and estimate for the standard deviation s. The normal deviate of the value, t, is defined

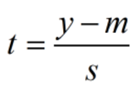
If s is equal to the true standard deviation of the distribution, the probability Pn that y is within the distribution can be determined with a normal distribution provided by the Probability function as follows:

Pn=Probability(-t, t, 0, 1)

However, when the standard deviation is not known, an estimate for the standard deviation, s, is obtained from n observations. The mean is also determined from these observations, so that the degrees of freedom is then n-1. In this case, the probability is given by

Pt=Students_t(t,degfreedom)

Notes:

1. The probability is a value between 0 and 1 that corresponds to the shaded area c in the figure.

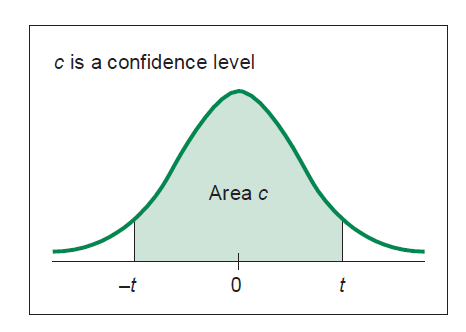
2. The Student_t function can be used in an inverse manner in which the the probability is specified and used to determine the t value, as shown in the example.

Example:

Determine the value of t that will result in a confidence level of 0.9 with 6 degrees of freedom.

P=0.9 "P is the confidence level"

df=6 "degrees of freedom"

P=Students_t(t,df) "t is determined from this function call"

P2=Probability(-t,t,0,1) "P2 the confidence level that would result if the degrees of freedom approaches infinity"

{Solution:

P2=0.948

t=1.943 }