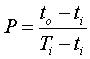 ,
, 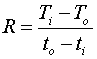
Log Mean Temperature Difference
LMTD_CF returns the correction factor needed to determine the log mean temperature difference (LMTD) of a heat exchanger with a flow configuration other than counterflow. LMTD_CF is 1 by definition for counterflow but it will be less than one for other flow configurations as presented in section 8.2 of Nellis and Klein.
The general form is: F=LMTD_CF(TypeHX$,P,R)
Inputs:
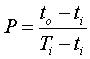 ,
, 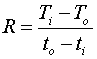
where
Ti and To, and ti and to are the temperatures at the inlet and outlet of the two streams respectively.
TypeHX$ - specifies the heat exchanger flow configuration; applicable heat exchanger geometries are listed below
The heat exchanger flow configuration, TypeHX$, must be set to one of the following (case-insensitive) strings:
'parallelflow'
'crossflow_both_unmixed'
'crossflow_one_unmixed'
'shell&tube_N' {where N is an integer between 1 and 9, specifying the number of shell pass. The number of tube passes is then, 2N, 4N, 6N, .... . }
Function LMTD_CF calls HX to determine the NTU of the heat exchanger, which is then used to determine LMTD_CF. The log mean temperature difference is valid, in general, for all values of R and from 0<P<1. However, at a particular value of R, it is possible to choose a value of P for which no value for F exists. In this case, the error shown may appear as: 'There is no solution for Ntu given epsilon = ___'.
There is no analytical solution to NTU given epsilon for the 'crossflow_both_mixed' flow configuration. In this case, a subprogram is internally called to solve for NTU in an iterative manner given the effectiveness.
$UnitSystem SI K Pa J
$TabStops 2 in
TypeHX$='crossflow_both_unmixed'
T_h_i=400 [K] "unmixed fluid inlet temperature"
T_h_o=330 [K] "unmixed fluid inlet temperature"
t_c_i=300 [K] "mixed fluid inlet temperature"
t_c_o=325 [K] "mixed fluid outlet temperature"
P=(t_c_o-t_c_i)/(T_h_i-t_c_i)
R=(T_h_i-T_h_o)/(t_c_o-t_c_i)
F=lmtd_cf(TypeHX$,P,R)
{Solution:
F=0.9329
}